2008 Winter Scripting Games Event 2
If you aren't already in the know, these ten problems are from the 2008 Winter Scripting games.
For each problem, I'm going to quickly sum up the interesting (interesting TO ME) bits of each problem, then I'm going to post the full source.
Event 2: Skating on Thin Ice
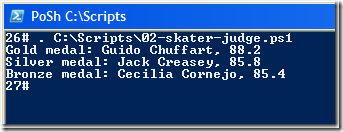
Here we do some very basic number crunching: read in scores, cut off the small and the large score, calculate the average. Then sort the results and print the top three.
Actually, in describing this I realize that this is a mostly boring problem. Check out how I use PowerShell's support of collections to chop off parts of them, sort, etc. Otherwise, there's not much here.
I will also point out that many of my solutions are excessively Object Happy. I.e., whenever possible, I construct an object with properties. Most of these times (with the exception of the blackjack game, #10, and the election runoff, #3 immediately below), objects were unnecessary. So, let this be your warning.
Source
function Create-SkaterObject ($skaterName, $skaterScore)
{
$o = new-object PSObject
Add-Member -inputObject $o -memberType NoteProperty -name "Name" -value $skaterName
Add-Member -inputObject $o -memberType NoteProperty -name "Score" -value $skaterScore
#POSTSCRIPT - ok, this scriptmethod is clearly gratuitous
Add-Member -inputObject $o -memberType ScriptMethod -name "NameAndScore" -value { "$($this.Name), $($this.Score)" }
$o
}
$totalScores = 7
function Calculate-Score ($scores)
{
$thisSkatersTrimmedScores = $scores | sort | select -first ($totalScores - 1) | select -last ($totalScores - 2)
$total = 0
foreach ($score in $thisSkatersTrimmedScores)
{
$total += $score
}
$total / ($totalScores - 2 )
}
function Get-SkaterScores ($filename)
{
$skaterRawData = cat $filename
$scores = @()
foreach ($skater in $skaterRawData)
{
$column = $skater.Split(",")
$thisSkaterName = $column[0]
$thisSkatersScores = @()
for ($i = 1; $i -lt $column.Count; $i++)
{
$thisSkatersScores += $column[$i]
}
$finalScore = Calculate-Score -scores $thisSkatersScores
$scores += Create-SkaterObject -skaterName $thisSkaterName -skaterScore $finalScore
}
$scores
}
$medals = @( "Gold", "Silver", "Bronze" )
function Solve-Problem2
{
$allScores = Get-SkaterScores -filename "C:\Scripts\skaters.txt"
$topScores = $allScores | sort Score -desc | select -first 3
$i = 0
foreach ($medal in $medals)
{
write-host "$medal medal: $($topScores[$i].NameAndScore())"
$i++
}
}
Solve-Problem2
2008 Winter Scripting Game Events: Index
- Introduction: TOTAL DOMINATION!
- Event 1: Could I Get Your Phone Number?
- Event 2: Skating on Thin Ice
- Event 3: Instant (Runoff) Winner
- Event 4: Image is Everything
- Event 5: You Call That a Password?
- Event 6: Prime Time
- Event 7: Play Ball!
- Event 8: Making Beautiful Music
- Event 9: You're Twisting My Words
- Event 10: Blackjack!
- Recap
 Peter Seale's weblog
Peter Seale's weblog